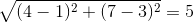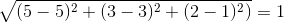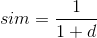如果你在运营一个2C的平台，那么你肯定关心用户流失的问题。腾讯有个产品叫信鸽Pro，它能够通过对用户往期行为的挖掘，预测用户潜在的流失（付费）行为，进而实现精准营销。据说，腾讯自己的手游就是用这个系统做用户分析的。

信鸽Pro获取大量用户数据，提取用户特征，然后通过算法建模，评估出用户可能的行为。算法建模中最基础的一步就是对用户进行分类。这里就介绍一种常用的分类算法 － 逻辑回归。

模型

用户数据比较复杂，这里用平面上的点举例。假设平面上有一些点，如图所示：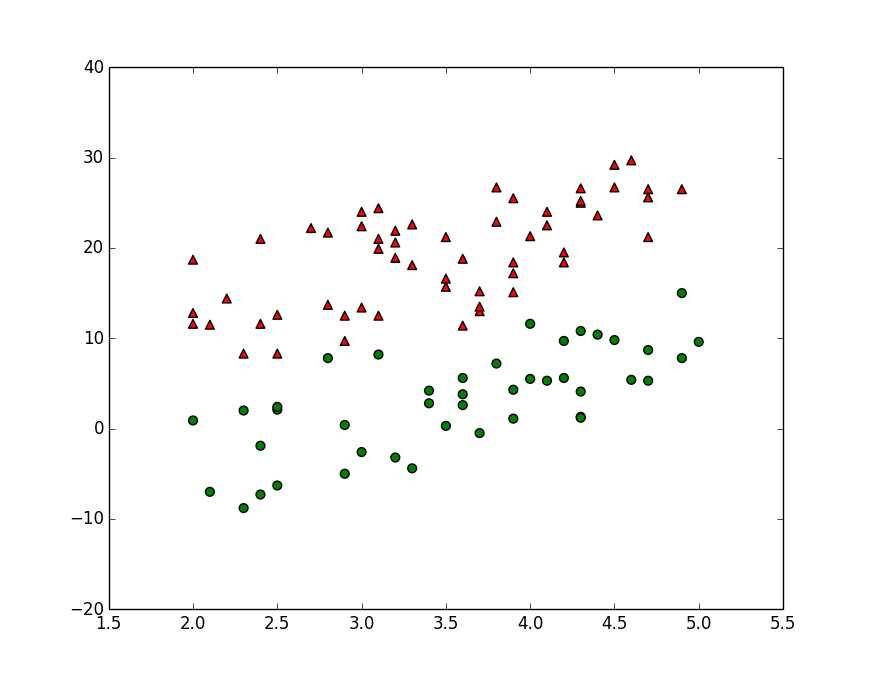

整个平面上只有两种图形，一种是三角形，另一种是圆形。可以把它们想象为两种不同的用户，比如活跃用户／非活跃用户。
问题：如果随意在这个平面新增加一个点, 比如点P(5,19)，那怎知把它归到哪一组更合适？可以想象为对新用户的预测。

思路

我们发现，三角形大都位于左上方，而圆形大都位于右下方。我们可以用尺子在图上画一条直线，该直线尽可能的将三角形和圆形分到两边。然后观察新点位于哪一侧。若与三角形在同一侧，则它应该属于三角形；若位于圆形一侧，则应属于圆形。在本例中，坐标P应该属于三角形更合适。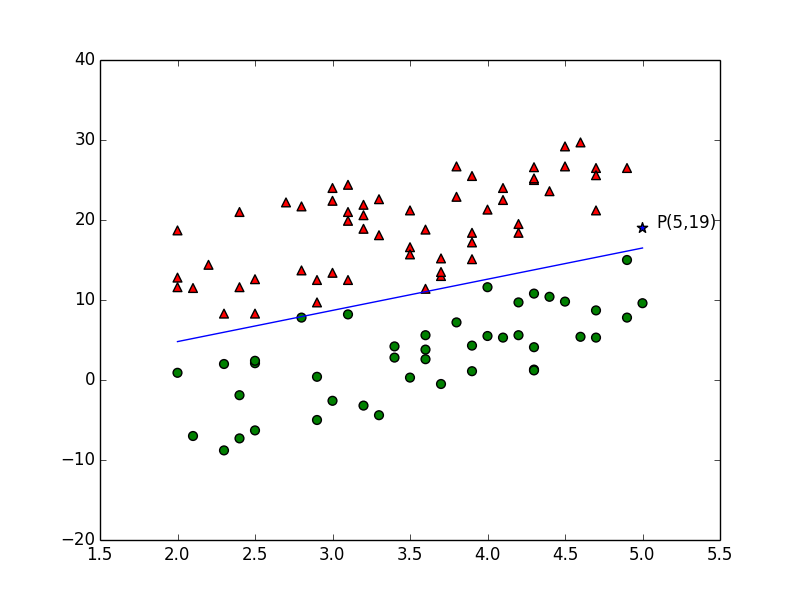

这个问题似乎很简单。但是，如果三维空间存在类似的问题，答案就没有那么显而易见了。那4维空间呢? 1024维空间呢?

不过别担心！借助计算机算法，N维空间分类的问题已经很容易解决，逻辑回归就是常用的一种。

逻辑回归

逻辑回归的核心思想就是通过现有数据，对分类边界线建立回归公式，以此进行分类。

在介绍算法之前，需要先介绍一个函数: Sigmoid函数。

Sigmoid函数

Sigmoid函数的表达式为：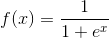

在坐标系中的图形为：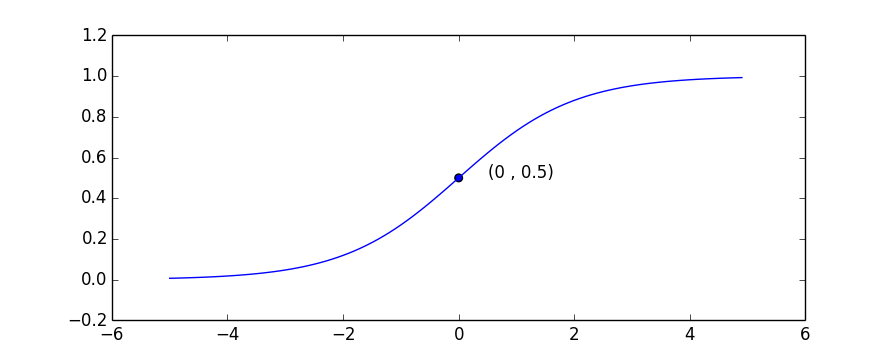

x>0时，x越大y越接近于1；x<0时，x越小，y越接近于0。如果把坐标拉长，曲线中间就会很“陡”。直观上x的“轻微”变化，都会导致y接近于0或1。

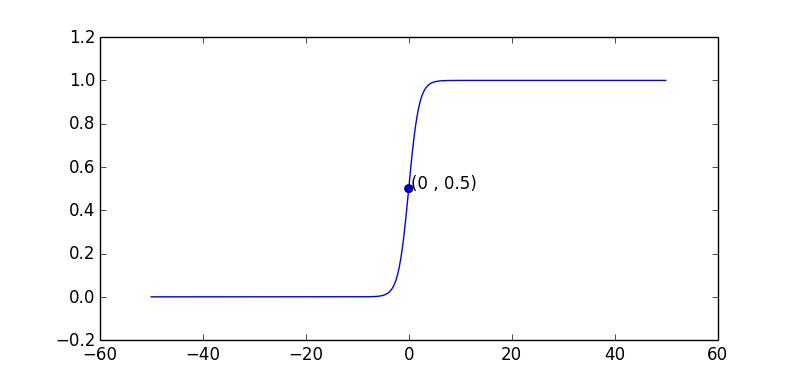
Sigmoid函数的作用是将任意实数转换成0～1的数，而0和1刚好可以用做分类，比如，用1表示三角形，用0表示圆形。小于0.5的可以划分为0类，大于0.5的划分为1类。（注：Sigmoid是单调增长函数，因而多个数字通过Sigmoid转换后相对位置不变，这是选择该函数的重要原因。）

分析步骤

简化模型

为便于分析，把模型中的坐标简化一些。下面的六个坐标点和一条分割线：

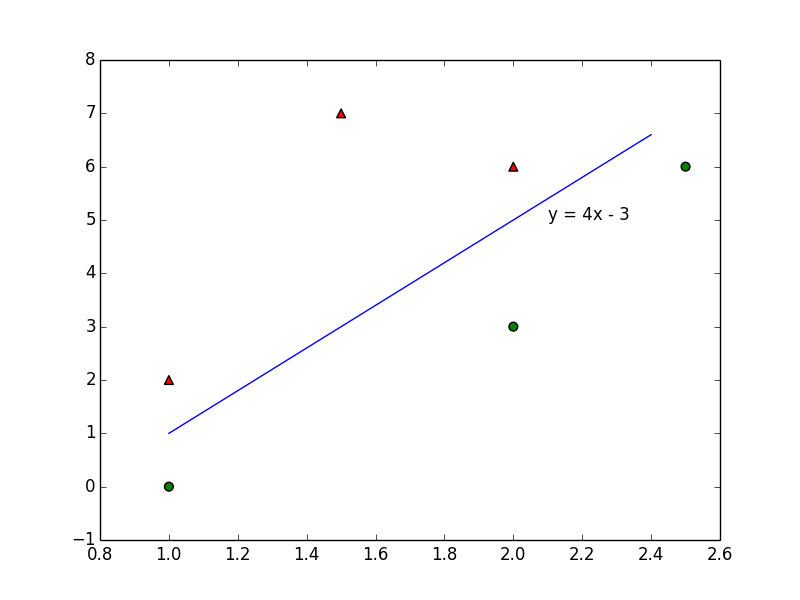
其中红色三角形坐标分别是(1,2)、(1.5,7)和(2,6)。绿色圆点坐标分别是（1,0）、(2,3)和(2.5,6)。分割线的函数为y=4x-3. 它的形式还可以转换成：3-4x+y=0 。

我们设表达式f(x,y) = 3-4x+y

把六个点的坐标代到这个方程式里,有

<表1>

(注：标识1表示三角形；标识0表示圆形)
f(x,y)>0的点在分割线上方，是三角形；f(x,y)<0的点在分割线下方，是圆形.

如果有个三角形的坐标是(2,4.5),那这个点的f(x,y)值等于-0.5，这个点就被分割线错误划分了。

现在的问题是，我们只有一些坐标以及这些坐标的分类信息，如何找到一条最优的分割线,使得尽可能少的点被错误划分？

损失函数

损失函数 (Loss Function) 的作用是判断直线错误划分数据的程度。一种方法是计算被错误划分的点的个数，错误点越少，直线越好。但，这种方法很难优化。另一种方法是计算点到直线的距离。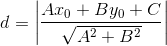

如果是一个平面来划分三维空间的点，那距离公式为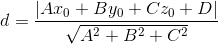

一般的，n维空间上一个点到超平面的距离为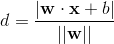

w是超平面的参数向量,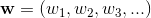

x是超平面的自变量,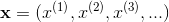

b是截距

超平面函数：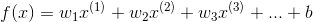
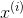表示x向量的第i个元素（特性）；后面会用到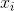，表示空间中的第i个点。

为了方便计算，一般在x中增加一个元素1，w中增加一个元素w0=b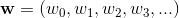


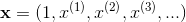
于是超平面函数变为：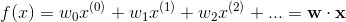

距离公式变为：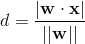

超平面上方的点f(x)>0, 下方的点f(x)<0,因此点到超平面的距离（分正负）: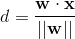

d是一个负无穷到正无穷的数。

通过sigmoid函数，将d变成一个0～1的值，设h = sigmoid(d)。若d为正且越大，h越接近于1，也就越应该属于三角形（分类1）；若d为负，且绝对值越大，h越接近于0，该点也就越应该属于圆形(分类0)。因此，h越接近于分类标识，划分的准确性越高。

设第j个点的分类表示为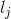，那么下面的公式就表示点j被错误划分的概率。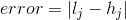

我们把损失函数设定为所有点被错误划分的平均概率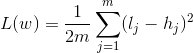

平方是为了保证概率为正，前面的1/2是为了求导数后消除参数。

那么，问题转化成：找到w的一个值，使得损失函数的值最小。

用梯度下降法求w

所谓梯度，就是函数在某个点增长最快的方向，有时称为斜度。如果函数是一个曲线，某个点的梯度就是该点的斜率，或导数。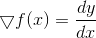


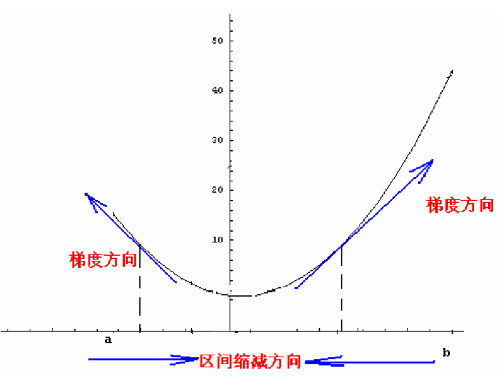
如果是曲面，梯度是在两个方向上求偏导。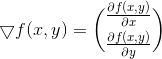

梯度下降法的核心思想是：欲求函数的最小值，先从某一点出发，沿着函数的梯度的反方向探寻，直到找到最小值。设每次探寻Delta(w)，步长为alpha，则梯度下降的算法的公式为：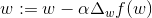

求导

用梯度下降法需要先对损失函数求导，我们的损失函数被分成三部分：

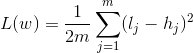• ——— (1)
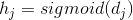• ——— (2)
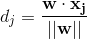• ———- (3)

可以通过复合函数求导法对损失函数求偏导：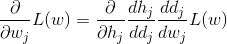

梯度公式重点关注的是导数的符号，所以这里可以简化一下。函数（2）是单调递增函数，所以导数是正数，不影响整体导数的符号，可以去除。 公式（3）的分母是正数，也不影响导数的符号，也可以去掉。最后得：

代入梯度下降算法公式得：

1/m为正数，也可用去掉。

代码

loadData()函数返回坐标值和分类标识。第一个返回值取前三列 x0,x1,x2；第二个返回值取第四列，即label

1
2
3
4
5
6
7
8
9
10
11
12
13

#coding:utf-8
from numpy import *

def loadData():
  data = [[1, 1, 2, 1],
          [1, 2, 6, 1],
          [1, 1.5, 7, 1],
          [1, 1, 0, 0],
          [1, 2, 3, 0],
          [1, 2.5, 6, 0]]
  ds = [e[0:3] for e in data]
  label = [e[-1] for e in data]
  return ds, label

Sigmoid函数

1
2

def sigmoid(x):
    return 1.0/(1+exp(-x))

梯度下降算法
input ds: 坐标数据; label: 标签
return w: 系数向量, nx1的矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def reduce(ds, label):
  #转换成矩阵
  dmat = mat(ds)
  lmat = mat(label).T
  #mxn的矩阵的行数和列数
  m,n = shape(dmat)
  #步长
  alpha = 0.1
  #循环次数
  loops = 200
  #初始化w为[1,1,1],即分割线为 1+x+y=0
  w = ones((n,1))
  for i in range(loops): 
    h = sigmoid(dmat*w)
    err = (h - lmat)
    w = w - alpha * dmat.T* err 
  return w.A[:,0]

测试

1
2
3

def test():
  ds,l = loadData()
  print reduce(ds,l)

运行结果

1

>>> import lr
>>> lr.test()
[ 3.1007773  -5.54393712  1.60563033]

也就是说w=(3.1, -5.5, 1.6), 即w0=3.1, w1=-5.5, w2 = 1.6

分割线的表达式为：w0+w1x+w2y=0， 代入w后得 3.1-5.5x+1.6y=0, 即y=3.44x-1.9 。 见下图，该直线正确地将图形划分开。

执行过程

w的初始值为(1,1,1),也就是0号线。
每次循环都会调整分割线的位置，执行到第200次的时候，分割线已经能够很好对坐标分组了。
<分割线调整图> 线编号n表示第n次调整(循环)之后的位置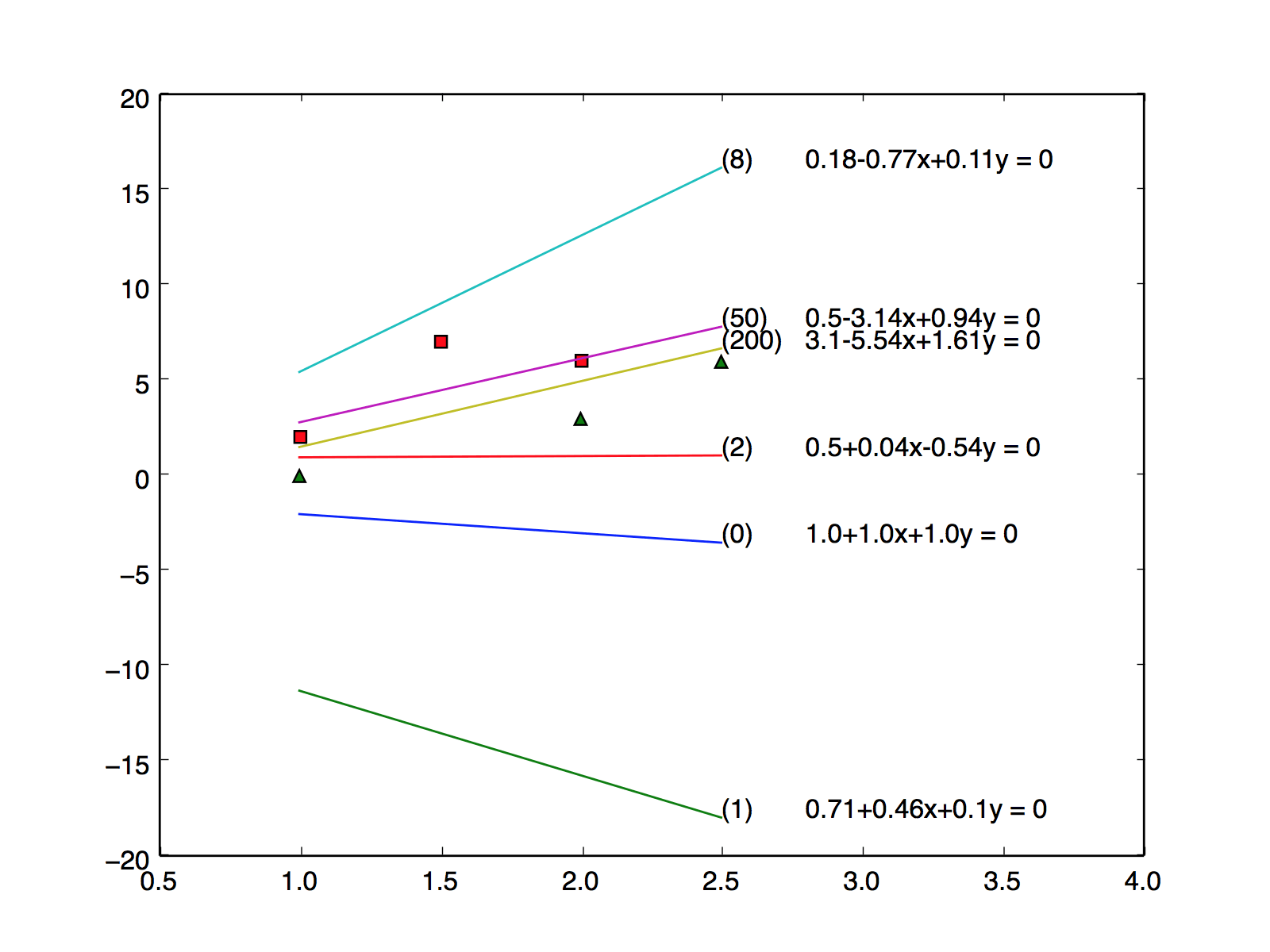

应用

把上面的x,y转换成用户特征，比如登录时间，登录频率等等。把三角形和圆形转换成付费用户和免费用户，就得到了付费用户预测模型；把三角形和圆形转换成流失用户和有效用户，就得到了流失用户预测模型。
当然，这只是个理论模型，实际应用要比这复杂的多的多。

拟合

所谓拟合是指已知某函数的若干离散函数值{f1,f2,…,fn}，通过调整该函数中若干待定系数f(λ1, λ2,…,λn)，使得该函数与已知点集的差别(最小二乘意义)最小。

在一些大型购物网站，我们常会看到一个功能叫“猜你喜欢”（或其它类似的名字），里面列出一些跟你买过商品相关的其它商品。网站的用户越多，或你在网站上购买的东西越多，它往往就猜的越准。在一些音乐网站、书评网站、电影网站也有类似的推荐系统，比如豆瓣上的“豆瓣猜”、百度音乐的“为你推荐”等，推荐结果都不错。

这些推荐系统的具体实现我们无法知晓，但原理是类似的，都是采用基于协同过滤的推荐机制。这里我们探讨一下这个推荐机制的原理。

举例

下图是一个用户对课程评分表。评分从1星到5星，灰色表示该用户没有对该课程评分。由图可知，用户3没有学过《面向对象基础》和《Struts开发框架》。问，如果要给用户3推荐其中一门课程，应该推荐哪一门？

基本概念

相似度

如果一个用户喜欢一种物品，那么他很可能也喜欢类似的物品。如果我们找到了测量物品之间相似程度的方法，也就解决了推荐系统的核心问题。

那如何找出这些方法呢？比如，啤酒与芝麻酱更相似还是与纸尿裤更相似？怎么知道啤酒和纸尿布的相似度是多少？

解决这个问题之前，不妨先考虑一个简单的问题。假设平面上有3个点，坐标分别是A(1,2)、B(1,3)和C(4,7)，如图：

AB的距离＝

BC的距离＝

很显然B与A的距离小于B与C的距离，换句话说B与A更接近(相似)。

这种用根方差计算出来的距离叫欧式距离，欧式距离可以扩展到多维空间。大于3维的空间我们想象不出来，但是算法是一样的。

如果我们有下面的数据

那么通过用欧式距离公式可知：

《机器学习》与《python编程》的距离＝

为了便于理解和比较，一般将相似度的值设在0到1之间，用欧式距离d得出的相似度可以表示为:

除了用欧式距离计算相似度外，常用的方法还有皮尔逊相关系数(Pearson correlation)和余玄相似度(cosine similarity).

下面是一段python代码，实现了基于欧式距离的相似度计算

1
2
3
4
5

from numpy import *
from numpy import linalg as la

def eSim(A,B):    
  return 1.0/(1.0+la.norm(A-B))

再添加一个加载数据的方法。该方法返回一个二维数组，表示用户对课程的评价值。

1
2
3
4
5
6
7
8

def loadData():    
  return[[5, 3, 0, 2, 2],
         [4, 0, 0, 3, 3],
         [5, 0, 0, 1, 1],
         [1, 1, 1, 2, 0],
         [2, 2, 2, 0, 0],
         [1, 1, 1, 0, 0],
         [5, 5, 5, 0, 0]]

推荐引擎 － 给用户推荐最喜欢的课程

目的：给定一个用户，程序返回N个该用户最喜欢的课程

步骤

• 查询用户没有评级的课程, 即矩阵中的0元素
• 在用户没有评级的所有课程中，对每个课程预测一个评级分数
• 评分从高到底排序, 返回前N个课程

推荐引擎需要一个对课程评估分值的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

'''
  函数功能：在给定相似度计算方法的条件下，估计该用户对课程的评分值
input
  ds: 评价矩阵
  userIdx: 用户编号
  simFunc: 相似度计算方法
  courseIdx: 课程编号
output
  编号为courseIdx的课程对应的估计分值 
'''
def standEst(ds, userIdx, simFunc, courseIdx):
    n = shape(ds)[1] #课程数量
    simTotal = 0.0; ratSimTotal = 0.0
    #遍历所有课程
    for j in range(n):
        userRating = ds[userIdx,j]  #用户对第j个课程的评价
        if userRating == 0: continue  #用户没有对该课程评分，跳过
        #寻找两个用户都评级的课程
        overLap = nonzero(logical_and(ds[:,courseIdx].A>0, ds[:,j].A>0))[0]
        #如果两个课程(courseIdx和j)没有共同评价人，则相似度＝0
        if len(overLap) == 0: similarity = 0
        #否则，计算相似度
        else: similarity = simFunc(ds[overLap,courseIdx], ds[overLap,j])
        #总相似度(相似度可以理解为权重)
        simTotal += similarity
        #相似度*评分的合计
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal #预计得分

推荐引擎代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

'''
推荐引擎: 给用户推荐N个最喜欢的课程
input
  ds: 评价矩阵
  userIdx:
  N: 最高推荐N个结果
  simFunc
  estFunc
'''
def recommendCourses(ds, userIdx, N=3, simFunc=eSim, estFunc=standEst):
    unratedCourses = nonzero(ds[userIdx,:].A==0)[1] #当前用户没有打分的课程 
    if len(unratedCourses) == 0: return '你已经学过所有课程'
    courseScores = [] #课程分数列表
    for courseIdx in unratedCourses:
        estimatedScore = estFunc(ds, userIdx, simFunc, courseIdx)
        courseScores.append((courseIdx, estimatedScore))
    return sorted(courseScores, key=lambda jj: jj[1], reverse=True)[:N]

测试函数，给用户3推荐课程

1
2
3

def test():
  dataMat = mat(loadData())
  print recommendCourses(dataMat,2)

执行代码

1
2
3

>>> import recommend
>>> recommend.test()
[(2, 3.6666666666666665), (1, 2.068764098505754)]

推荐结果：下标为2的课程（《Struts开发框架》）得分3.67星，下标为1的课程（《面向对象思想》）得分为2星。因此，判断用户更喜欢《Struts开发框架》。

从直观上也可以这样理解：用户4，5，6，7都对《Java编程》和《Struts开发框架》做了评价，而且评价相同。因此，《Struts开发框架》与《Java编程》属于非常相似的物品。 而用户3对《Java编程》评价极高（5星），故判断《Struts开发框架》也应该得高分（对于用户3而言）。

局限

• 这个算法需要对整个数据集进行多次复杂的计算，如果数据量很大，则性能可能无法接受。一种解决办法是对矩阵进行SVD分解，把高维度的矩阵转换成低维度度的矩阵。此外，采用离线计算，将相似度这个中间结果保存起来重复利用也可以提高性能。
• 冷启动问题。新课程加进来时，由于缺乏数据无法进行推荐。这个可以通过给课程打标签的方式进行。